[파생변수 활용]
1. 파생 변수의 개념
1) 파생 변수의 정의
- 작위적(의도적) 정의에 의해 특정 의미를 갖는 변수
- 사용자가 특정 조건을 만들어 의미를 부여한 변수
2) 파생 변수의 성격
- 주관적: 논리적 타당성을 갖추지 못한 경우, 분석과 해석에 문제가 생김
- 특정 상황에만 의미있는 것이 아닌, 대표성이 나타나도록 변수 설계를 해야 함.
ex) 2021년 하반기 제품 구매 고객 리스트(X) -> 하반기 제품 구매 고객 리스트
- 세분화, 고객행동 예측, 마케팅 혹은 캠페인 반응 예측에 활용이 가능
ex) 변수(근무시간 중 구매정도, 주거래매장, 선호상품, 가격대 등) -> 고객의 예상 구매 빈도, 거래 금액으로 고객 등급 분류, 캠페인 시행 효과 확인 등
2. 파생 변수의 예시와 활용
1) 제작
- 변수를 조합하거나, 함수를 적용해 새로운 변수를 생성
2) 요약변수
- 기본 정보를 특정 기준으로 그룹핑하여 요약한 변수
- 예) 연속형 변수의 구간화, 사용 단어 빈도, 기간별 구매 금액 등
- 특성
- 수집된 정보를 분석에 맞게 종합
- 데이터 마트(데이터 원 저장소인 데이터 웨어하우스와 사용자 사이의 복제된 데이터)에서 가장 기본적인 변수
- 다수의 모델에 공통으로 사용될 수 있어, 재활용성이 높음
- 간단한 구조(자동화 프로그램 구축 가능)
- 데이터마트: 일반적으로 각 응용분야별로 구축되는 소규모 형태의 데이터웨어하우스
(의사결정지원시스템(DSS: Decision Support System): 사용자의 요구사항에 초점을 맞춘, 특정 사용자 집단에 특화된 데이터 저장고)
| 데이터웨어하우스(DW) | 데이터마트 | |
| 범위 | 애플리케이션 중립적 중앙집중식 공유 전사적 |
특정 애플리케이션 특정 부문 특정 사용자 영역 비즈니스 프로세스 중심적 |
| 주제영역 | 다수의 데이터 구조 지원 | 단일한 부분적 데이터 구조 지원 |
| 데이터 관점 | 오랜 기간의 상세 데이터 요약 (시계열 이력 데이터, 납입보험료) |
제한된 규모의 데이터 요약 (추세, 패턴 분석) |
| 기타특성 | 지속성/전략적 | 프로젝트 중심 |
- 요약변수 사용 사례
* 기간별 구매 금액/횟수: 고객의 구매패턴 식별
* 위클리 쇼퍼: 구매 시기를 통해 고객의 특성을 추정
* 상품별 구매금액/횟수: 고객의 라이프 스테이지/라이프스타일 등을 이해
* 유통 채널별 구매금액: 온/오프라인 고객의 구매를 유도
* 단어 빈도: 텍스트자료에서 단어들의 출현 빈도를 데이터화하여 사용
* 초기 행동변수: 고객 가입/첫 거래 초기 1개월간 거래 패턴 -> 1년 후 반응 예측
* 트렌드변수: 추이값을 나타내는 변수
* 결측값과 이상값 처리: 내용 파악 후 처리
* 연속형 변수의 구간화: 분석 후 적용 단계를 고려한 데이터 분석을 위해 연령/비용 등 연속형 변수를 구간화 하는 것
3) 파생변수
- 사용자가 의미를 부여하여 생성한 변수
- 주관적(논리적 타당성이 필요)
- 생성된 변수가 모집단의 대표성을 나타낼 수 있어야함
- 파생변수 사용 사례
* 근무시간 구매 지수: 근무시간대에 거래가 발생하는 비율을 산출
* 주 구매 매장 변수: 고객의 주거래 매장을 예측
* 주 활동 지역 변수: 고객의 정보/거래내용 통해 주 활동 지역을 예측
* 주 구매 상품 변수: 상품 추천에 활용
* 구매 상품 다양성 변수: 고객의 구매 성향 파악
* 선호하는 가격대 변수
* 라이프 스테이지 변수
* 라이프 스타일 변수
* 행사 민감 변수
- 파생 변수의 활용
* 모델 성능 향상의 방법
1. 주어진 데이터를 가지고, 모델에 맞춰 데이터를 수정하고, 주요 변수에 따라 모델링을 함(일반적인 방법)
2. 데이터의 특성에 대해 이해하고, 분석자의 주관에 따라 파생변수를 얼마나 잘 생성하느냐에 따라 모델의 성능은 향상됨
3. R을 이용한 파생변수 실습
* melt(): 식별자 id, 측정 변수 variable, 측정치 value 형태로 데이터를 재구성하는 함수
reshape2::melt.data.frame(
data, # melt할 데이터
id.vars, # 식별자 컬럼들
measuer.vars, # 측정치 컬럼들
na.rm = False # NA인 행을 결과에 포함시킬지 여부. False는 NA를 제거하지 않음
)ex) melt1 = melt(data, id = 'names') # names 변수를 id변수로 재구성
* cast(): 새로운 구조로 데이터를 만드는 함수(melt_Data, 변수1, 변수2 ~ column 생성 변수명)
* dplyr 패키지: 데이터 프레임을 처리하는 함수로 구성된 패키지
- data.table
- 각종 데이터베이스: MySQL, PostgreSQL, SQLite, BigQuery 지원
- 데이터 큐브: dplyr 패키지 내부에 실험적으로 내장됨
| 함수명 | 내용 | 유사함수 |
| filter() | 지정한 조건식에 맞는 데이터 추출 | subset() |
| select() | 열의 추출 | data[, c('Year', 'Month')] |
| mutate() | 열 추가 | transform() |
| arrange() | 정렬 | order, sort() |
| summarise() | 집계 | aggregate() |
* hflights 데이터: 미국 휴스턴에서 출발하는 모든 비행기의 2011년 이착륙기록이 수록된 것으로 227496건의 이착륙기록에 대해 21개 항목을 수집한 데이터
install.packages('dplyr')
install.packages('hflights')
library(hflights)
library(dplyr)
str(hflights) # hflights의 구조 출력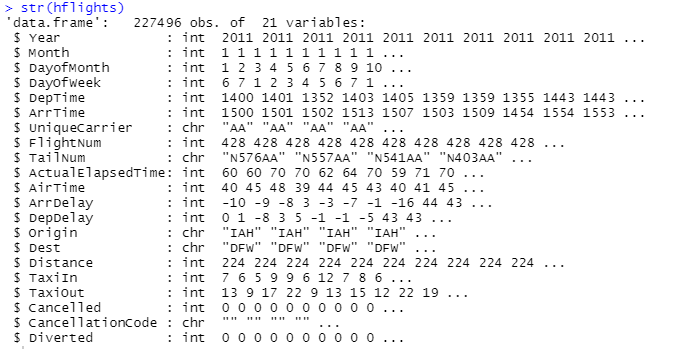
# 변수명 확인
colnames(hflights)
# 자료를 보기 좋게 한 화면에 편집
hflights_df <- tbl_df(hflights)
hflights_df
# 파생변수 추가(칼럼 추가)
aa <- mutate(hflights_df, gain=ArrDelay - DepDelay)
# 변수가 새로 생성된 것을 확인
aa
[앙상블 기법 활용]
1. 앙상블 기법의 개념
1) 앙상블 기법
- 정의: 주어진 자료로 여러 개의 예측 모델을 학습한 다음, 하나의 최종 예측 모델을 사용하여 정확도를 높이는 기법
(지도학습의 장/단점: 정교화, 대규모화되어 예측 성능이 뛰어나지만, 학습에 오랜 시간이 걸리고, 과도적합으로 인한 오차 증가가 동반된다.)
-> 지도학습 기법보다 더 좋은 성능을 내기 위해 고안된 기법(많은 기저 학습기들을 합치는 방법)
- 단점: 모형 복잡도가 높아 설명하기 어렵다
- 장점: 성능이 높다
- 트리 기반 통계적 학습 기법
| 트리 기반 통계적 학습 기법 | |
| 지도 학습 | 의사결정 트리 - 회귀/분류 트리 |
| + 배깅, 부스팅, 랜덤 포레스트 | |
| 비지도 학습 | 군집화(Clustering) |
2) 고려사항
- 학습기의 선택: 비교적 간단하면서도, 서로 차별성이 있는 분류기를 선택 => 결합을 통해 효과를 향상
1) 학습 알고리즘 차별화: 기법 결합 시, 베이즈 분류기와 k-neighbors 알고리즘, 인공신경망과 SVM을 결합하는 방법과 같이 서로 다른 접근 방법을 가진 알고리즘을 선택
2) 모델 선택과 관련된 파라미터의 차별화
3) 학습 데이터 차별화: 같은 기법 모델을 결합하되, 학습에 사용되는 데이터 집합에 차별을두어 복수 개의 분류기를 만드는 방법
- 결합 방법의 선택: 학습이 완료된 학습기들로부터 얻어지는 인식 결과의 결합 => 각 학습기의 특성을 고려하여 결합
* 병렬적 결합 방법: 기법 결합 시, 각각의 분류기로부터 얻어진 결과를 한 번에 모두 고려하여 최종 결과를 얻는 방법
* 순차적 결합 방법: 각 분류기의 결과를 단계별로 나누어, 단계적으로 결합하는 방법
-> 앞 단계에 배치된 결과가 뒤에 배치된 분류기의 학습과 분류에 영향을 미침
2. 앙상블 기법의 종류와 활용
1) 배깅 = Bootstrap(랜덤 샘플링) + Aggregating(집합)
- 최종 모델 생성 과정
1. 주어진 학습자료에서 표본을 무작위로 재추출 해, 여러 개의 부트스트랩을 만듬
(부트스트랩: 실측 데이터를 바탕으로 가상의 샘플링을 수행해, 분포를 추정하는 것)
2. 만들어진 부트스트랩 자료를 각각에 대해 추출 표본들의 분산을 표본 수로 나눔
3. 분산을 줄인 예측 모형 제작
4. 그 모형을 결합해 최종 모형을 생성
- 배깅 알고리즘: 각 훈련치를 평균하면, 분산을 낮추는 효과가 있음(분산을 낮춰 과적합을 막아줌)
2) 부스팅
- 정의: 제대로 분류되지 않은, 예측력이 약한 모형들을 결합하여 강한 예측 모형을 만드는 것
- 오차가 큰 학습기의 경우 가중치를 높이고, 오차가 작은 학습기의 경우 가중치를 낮춤
- 부스팅 알고리즘
* 직렬적 개념
* 훈련오차를 빠르고, 쉽게 줄일 수 있다.
* 잘못 분류된 데이터에 가중치를 부여하여 더 잘 분류하는 목적으로 사용
- 학습과정
학습데이터 -> 1st 분류기 -> 오분류/정분류 데이터 중 k개 추출 -> 2nd 분류기 학습 -> 오분류/정분류 데이터 중 k개 추출 -> 반복 -> ... -> 적용 데이터를 1st 분류기, 2nd 분류기, 3rd 분류기 등 적용 -> 최종 결과
3) 랜덤 포레스트
- 정의: 분산이 큰 의사결정나무의 단점을 통계적 기법으로 극복한 방법
- 여러 개의 의사결정 나무를 만들고, 각각의 나무에 부트스트랩을 이용해 생성한 데이터셋으로 모델을 구성함
=> 편향을 증가시킴으로써, 분산이 큰 의사결정나무의 단점을 완화
- 장점: 과적합 발생률이 낮아지고, 일반 의사결정나무보다 예측력이 높아진다
- 단점: 복잡한 구조로 해석력이 떨어짐
3. R을 이용한 앙상블 기법
1) 랜덤포레스트
install.packages('randomForest')
library(randomForest)
idx = sample(2, nrow(iris), replace = T, prob = c(0.7,0.3))
# sample = 분류 지표(예: 2 -> 1 or 2)
# prob = probability(예: c(0.7, 0.3) -> 1 = 70%, 2 = 30%)
idx
'''
[1] 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 2 1
[22] 1 2 1 1 1 1 2 1 2 1 2 1 2 1 1 1 2 1 2 1 1
[43] 1 1 2 1 1 1 2 1 1 1 2 1 1 2 2 1 1 1 1 1 1
[64] 1 2 1 2 2 2 1 1 1 1 2 1 2 1 2 1 1 1 2 2 1
[85] 1 2 2 2 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 1
[106] 1 2 2 2 1 2 1 1 1 1 1 1 2 1 1 2 1 1 1 1 2
[127] 2 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 1
[148] 1 2 1
'''
trainData = iris[idx == 1,]
testData = iris[idx == 2,]
model = randomForest(Species~., data = trainData, ntree = 100, proximity = T)
# ntree: 의사결정나무 갯수
model
- OOB(Out Of Bag)(estimate of error rate, 에러 추정치): 3.74%(모델 훈련에 사용되지 않은 데이터를 사용해 에러 추정)
- 의사결정나무 갯수(Number of trees): 100
- 혼동행렬을 통해 정분류, 오분류된 케이스 갯수를 알 수 있음
importance(model)
- 지니계수: 값이 높은 변수가 클래스를 분류하는데 가장 큰 영향을 줌
2) 기타
- 배깅은 party와 caret 라이브러리를 사용해서 부트스트랩과 모델링을 함
- 부스팅은 tree 라이브러리와 rpart 패키지를 사용하여 표본 추출과 트리 모델을 형성할 수 있음
'프로그래밍' 카테고리의 다른 글
| [HDFS] HDFS 명령어 및 운영 규칙 (0) | 2021.06.02 |
|---|---|
| [Linux] Linux 명령어 정리 & Hadoop 설치 및 환경 조성 (0) | 2021.06.02 |
| [R] R을 이용한 군집분석 (0) | 2021.05.29 |
| [R] R을 이용한 예측분석 (0) | 2021.05.29 |
| [R] R을 이용한 로지스틱회귀분석 (0) | 2021.05.24 |